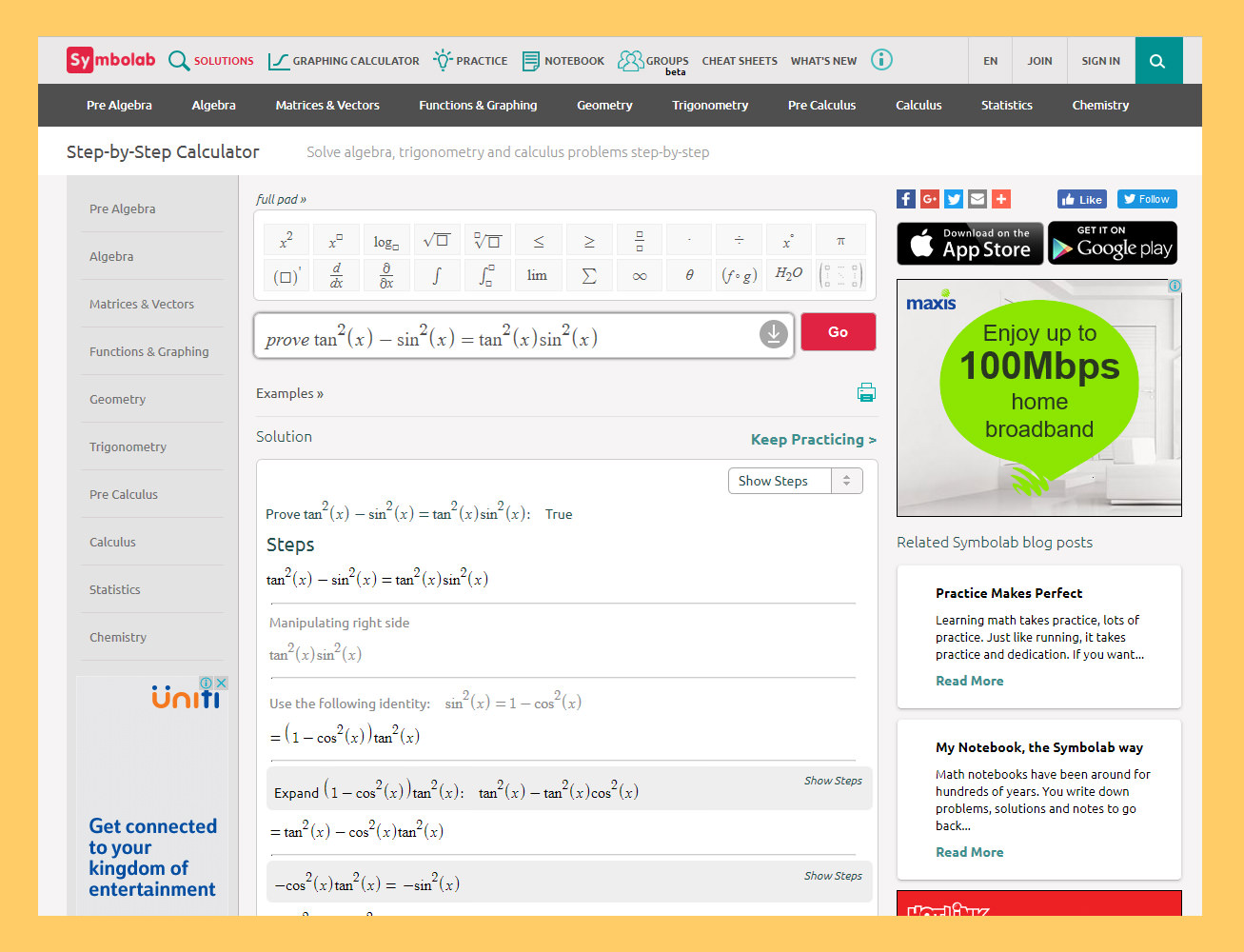
Partial Fraction Calculator Program
Rational fraction R ( x )is called the fraction of the form:If n. AdvertisementEach linear multiplier of the form, contained inQ m ( x )corresponds the decomposition of the form:Each quadratic multiplier of the form, contained inQ m ( x )corresponds to the decomposition of the form:Our online calculator finds partial fraction decomposition of any (proper, improper) rational fraction. Hip hop soul party album. If initial fraction is the improper one,(i.e. Order of polynomial in the numerator greaters of equals to the order of polynomial in the denominator) calculator divides numerator to the denominator andextracts the proper fraction. Partial fraction decomposition is usually used to of therational expressions.The example of the step by step solution ishere.
AnswerAs with the numerical fractions, we have to put the rational functions over a common denominator by multiplying each by a clever form of 1. Once the denominators are the same, we can add the numerators.We could continue to the next step, which would bebut we're not going to bother. We have the right form for the partial fractions technique when we get to the stepso we'll stop there.When adding rational functions for the sake of the partial fractions technique, we don't multiply things out. For example, when addingwe stop here:We also don't bother to write out the step where we multiply each fraction by a clever form of 1.
Polynomial Fraction Calculator
We just multiply the numerator of each fraction by the denominator of the other fraction, then add the results.If this doesn't make sense, we recommend reviewing how to add rational functions. If this does make sense, it's time to practice. AnswerThe denominator factors as2 x 2 – 5 x – 3 = ( x – 3)(2 x + 1)so the partial fraction decomposition will look likeAdd the partial fractions and set their numerator equal to the original numerator:8 x – 10 = A(2 x + 1) + B( x – 3).Set x = 3 and solve for A:8 x – 10 = A(2 x + 1) + B( x – 3)8(3) – 10 = A(2(3) + 1) + B(3 – 3)14 = 7 A2 = ANow set x = 0 and solve for B:8 x – 10 = A(2 x + 1) + B( x – 3)8(0) – 10 = (2)(2(0) + 1) + B(0 – 3)-10 = 2 – 3 B3 B = 12B = 4The decomposition is. AnswerThe denominator factors as-2 x 2 + 7 x + 15 = (2 x + 3)(5 – x)or as-2 x 2 + 7 x + 15 = (-2 x – 3)( x – 5).We'll go with-2 x 2 + 7 x + 15 = (2 x + 3)(5 – x)first. AnswerThe denominator factors into3 x 2 + x – 4 = ( x – 1)(3 x + 4)so the decomposition into partial fractions will look likeAdd the partial fractions and set the resulting numerator equal to the original numerator:25 x + 10 = A(3 x + 4) + B( x – 1).Set x = 1 and solve for A:25 x + 10 = A(3 x + 4) + B( x – 1)25(1) + 10 = A(3(1) + 4) + B(1 – 1)35 = 7 A5 = ASet x = 0 and solve for B:25 x + 10 = A(3 x + 4) + B( x – 1)25(0) + 10 = (5)(3(0) + 4) + B(0 – 1)10 = 20 – B10 = BThe decomposition is. AnswerWe didn't do this one yet.
Partial Fraction Calculator Programs
The denominator factors into-2 x 2 + 3 x – 1 = (-2 x + 1)( x – 1)so the partial fraction decomposition will look likeAdd the partial fractions and set the resulting numerator equal to the original numerator:-3 x + 1 = A( x – 1) + B(-2 x + 1).Set x = 1 and solve for B:-3 x + 1 = A( x – 1) + B(-2 x + 1)-3(1) + 1 = A(1 – 1) + B(-2(1) + 1)-2 = - B2 = BThen set x = 0 and solve for A:-3 x + 1 = A( x – 1) + B(-2 x + 1)-3(0) + 1 = A(0 – 1) + (2)(-2(0) + 1)1 = - A + 2A = 1The partial fraction decomposition isNow we can evaluate the integral.